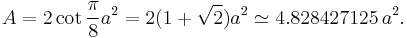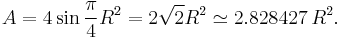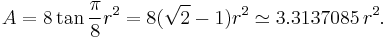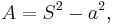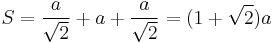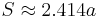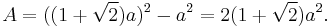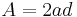Octagon

Regular octagon
A regular octagon
Type	general type of this shape
Edges and vertices	8
Schläfli symbol	{8} t{4}
Coxeter–Dynkin diagrams
Symmetry group	Dihedral (D₈)
Area	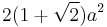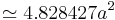$2(1%2B\sqrt{2})a^2$ $\simeq 4.828427 a^2$ (with a = edge length)
Internal angle (degrees)	135°
Properties	convex, cyclic, equilateral, isogonal, isotoxal

In geometry, an octagon (from the Greek okto, eight^[1]) is a polygon that has eight sides. A regular octagon is represented by the Schläfli symbol {8}.

1 Regular octagon
2 Construction
3 Standard coordinates
4 Uses of octagons
5 Derived figures
- 5.1 Petrie polygons
6 See also
7 References
8 External links

Regular octagon

A regular octagon is a closed figure with sides of the same length and internal angles of the same size. It has eight lines of reflective symmetry and rotational symmetry of order 8. The internal angle at each vertex of a regular octagon is 135° and the sum of all the internal angles is 1080° (as for any octagon). The area of a regular octagon of side length a is given by

$A = 2 \cot \frac{\pi}{8} a^2 = 2(1%2B\sqrt{2})a^2 \simeq 4.828427125\,a^2.$

In terms of R (circumradius), the area is

$A = 4 \sin \frac{\pi}{4} R^2 = 2\sqrt{2}R^2 \simeq 2.828427\,R^2.$

In terms of r (inradius), the area is

$A = 8 \tan \frac{\pi}{8} r^2 = 8(\sqrt{2}-1)r^2 \simeq 3.3137085\,r^2.$

These last two coefficients bracket the value of pi, the area of the unit circle.

The area can also be derived as follows:

$\,\!A=S^2-a^2,$

where S is the span of the octagon, or the second shortest diagonal; and a is the length of one of the sides, or bases. This is easily proven if one takes an octagon, draws a square around the outside (making sure that four of the eight sides touch the four sides of the square) and then taking the corner triangles (these are 45–45–90 triangles) and placing them with right angles pointed inward, forming a square. The edges of this square are each the length of the base.

Given the length of a side a, the span S is:

$S=\frac{a}{\sqrt{2}}%2Ba%2B\frac{a}{\sqrt{2}}=(1%2B\sqrt{2})a$

$S \approx 2.414a\,$

The area is then as above:

$A=((1%2B\sqrt{2})a)^2-a^2=2(1%2B\sqrt{2})a^2.$

Another simple formula for the area is

$\ A=2ad$

where d is the distance between parallel sides (the same as span S in the diagram).

Construction

A regular octagon is constructible with compass and straightedge.

Standard coordinates

The coordinates for the vertices of a regular octagon centered at the origin and with side length 2 are:

(±1, ±(1+√2))
(±(1+√2), ±1).

Uses of octagons

Derived figures

Petrie polygons

The octagon is the Petrie polygon for these 12 higher dimensional uniform polytopes, shown in these skew orthogonal projections of in A₇, B₄, and D₅ Coxeter planes.

A₇	7-simplex	Rectified 7-simplex	Birectified 7-simplex	Trirectified 7-simplex
B₄	16-cell	Rectified 16-cell	Rectified tesseract	Tesseract
D₅	Trirectified demipenteract	Birectified demipenteract	Rectified demipenteract	Demipenteract

References

^ Shorter Oxford English Dictionary (6th ed.), Oxford University Press, 2007, ISBN 978-0-19-920687-2

External links

Octagon Calculator
Definition and properties of an octagon With interactive animation
Weisstein, Eric W., "Octagon" from MathWorld.

Regular polygons

Listed by number of sides

1–10 sides	Henagon (Monogon) Digon Equilateral triangle Square Pentagon Hexagon Heptagon Octagon Nonagon (Enneagon) Decagon

11–20 sides	Hendecagon Dodecagon Triskaidecagon Tetradecagon Pentadecagon Hexadecagon Heptadecagon Octadecagon Nonadecagon (Enneadecagon) Icosagon

Others	Triacontagon Chiliagon Apeirogon

Star polygons	Pentagram Hexagram Heptagram Octagram Enneagram Decagram Hendecagram Dodecagram

ph...oir